Estimating Monotonic Effects with brms
Paul Bürkner
2024-03-19
Source:vignettes/brms_monotonic.Rmd
brms_monotonic.RmdIntroduction
This vignette is about monotonic effects, a special way of handling discrete predictors that are on an ordinal or higher scale (Bürkner & Charpentier, in review). A predictor, which we want to model as monotonic (i.e., having a monotonically increasing or decreasing relationship with the response), must either be integer valued or an ordered factor. As opposed to a continuous predictor, predictor categories (or integers) are not assumed to be equidistant with respect to their effect on the response variable. Instead, the distance between adjacent predictor categories (or integers) is estimated from the data and may vary across categories. This is realized by parameterizing as follows: One parameter, \(b\), takes care of the direction and size of the effect similar to an ordinary regression parameter. If the monotonic effect is used in a linear model, \(b\) can be interpreted as the expected average difference between two adjacent categories of the ordinal predictor. An additional parameter vector, \(\zeta\), estimates the normalized distances between consecutive predictor categories which thus defines the shape of the monotonic effect. For a single monotonic predictor, \(x\), the linear predictor term of observation \(n\) looks as follows:
\[\eta_n = b D \sum_{i = 1}^{x_n} \zeta_i\]
The parameter \(b\) can take on any real value, while \(\zeta\) is a simplex, which means that it satisfies \(\zeta_i \in [0,1]\) and \(\sum_{i = 1}^D \zeta_i = 1\) with \(D\) being the number of elements of \(\zeta\). Equivalently, \(D\) is the number of categories (or highest integer in the data) minus 1, since we start counting categories from zero to simplify the notation.
A Simple Monotonic Model
A main application of monotonic effects are ordinal predictors that can be modeled this way without falsely treating them either as continuous or as unordered categorical predictors. In Psychology, for instance, this kind of data is omnipresent in the form of Likert scale items, which are often treated as being continuous for convenience without ever testing this assumption. As an example, suppose we are interested in the relationship of yearly income (in $) and life satisfaction measured on an arbitrary scale from 0 to 100. Usually, people are not asked for the exact income. Instead, they are asked to rank themselves in one of certain classes, say: ‘below 20k’, ‘between 20k and 40k’, ‘between 40k and 100k’ and ‘above 100k’. We use some simulated data for illustration purposes.
income_options <- c("below_20", "20_to_40", "40_to_100", "greater_100")
income <- factor(sample(income_options, 100, TRUE),
levels = income_options, ordered = TRUE)
mean_ls <- c(30, 60, 70, 75)
ls <- mean_ls[income] + rnorm(100, sd = 7)
dat <- data.frame(income, ls)We now proceed with analyzing the data modeling income
as a monotonic effect.
The summary methods yield
summary(fit1) Family: gaussian
Links: mu = identity; sigma = identity
Formula: ls ~ mo(income)
Data: dat (Number of observations: 100)
Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup draws = 4000
Regression Coefficients:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept 30.82 1.38 28.07 33.52 1.00 2259 2479
moincome 14.74 0.63 13.49 16.01 1.00 2223 2209
Monotonic Simplex Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
moincome1[1] 0.67 0.04 0.59 0.74 1.00 2110 1960
moincome1[2] 0.26 0.04 0.18 0.34 1.00 3509 2857
moincome1[3] 0.07 0.04 0.01 0.15 1.00 2752 1627
Further Distributional Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma 6.87 0.51 5.97 7.95 1.00 2743 2307
Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).
plot(fit1, variable = "simo", regex = TRUE)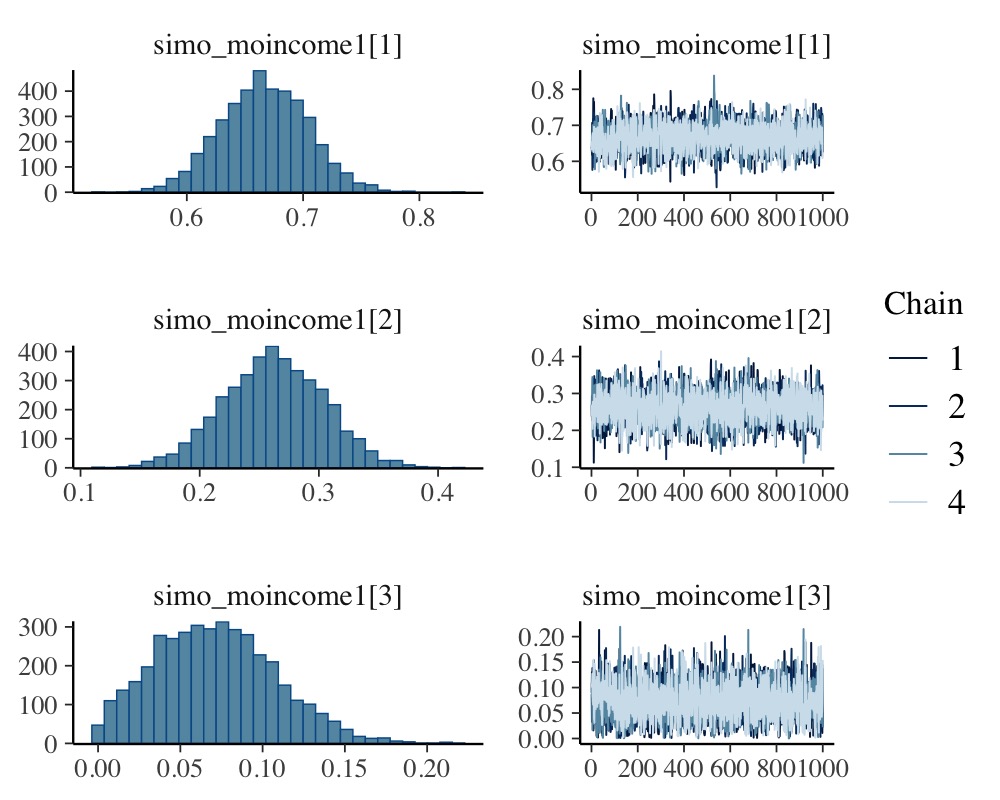
plot(conditional_effects(fit1))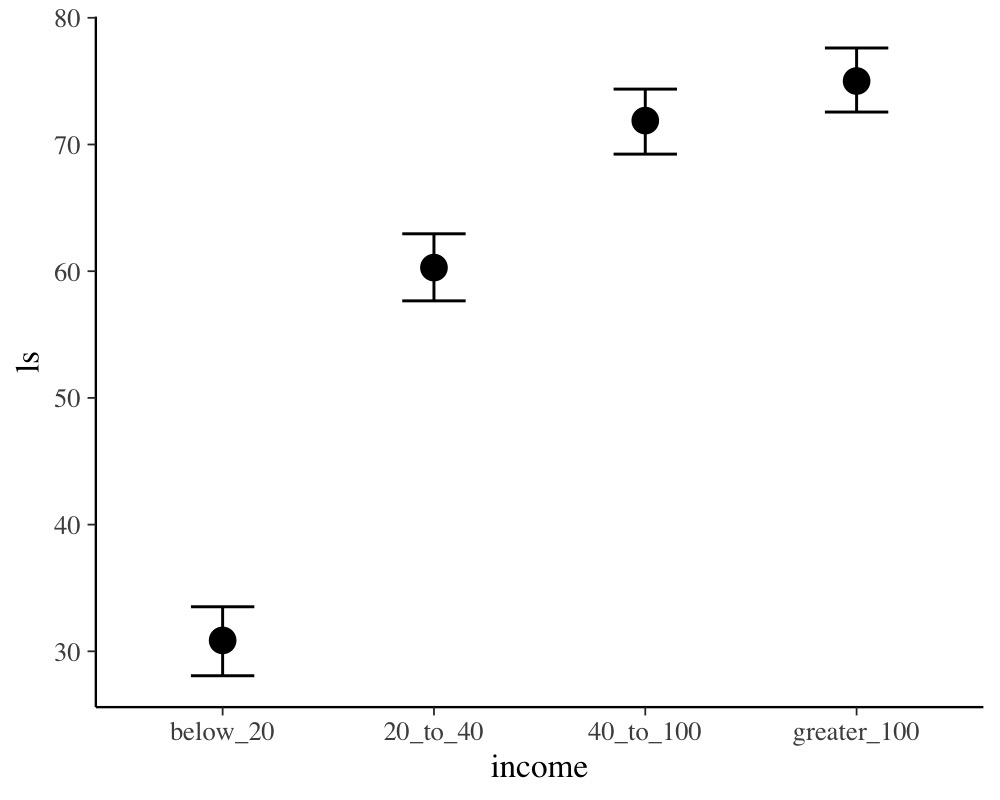
The distributions of the simplex parameter of income, as
shown in the plot method, demonstrate that the largest
difference (about 70% of the difference between minimum and maximum
category) is between the first two categories.
Now, let’s compare of monotonic model with two common alternative
models. (a) Assume income to be continuous:
dat$income_num <- as.numeric(dat$income)
fit2 <- brm(ls ~ income_num, data = dat)
summary(fit2) Family: gaussian
Links: mu = identity; sigma = identity
Formula: ls ~ income_num
Data: dat (Number of observations: 100)
Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup draws = 4000
Regression Coefficients:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept 23.91 2.40 19.12 28.64 1.00 3448 2918
income_num 14.36 0.89 12.61 16.09 1.00 3385 2908
Further Distributional Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma 9.72 0.69 8.49 11.17 1.00 3933 2787
Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).or (b) Assume income to be an unordered factor:
contrasts(dat$income) <- contr.treatment(4)
fit3 <- brm(ls ~ income, data = dat)
summary(fit3) Family: gaussian
Links: mu = identity; sigma = identity
Formula: ls ~ income
Data: dat (Number of observations: 100)
Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup draws = 4000
Regression Coefficients:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept 30.60 1.40 27.83 33.27 1.00 3147 2789
income2 29.72 1.90 26.01 33.43 1.00 3259 2968
income3 41.49 2.01 37.52 45.45 1.00 3455 2581
income4 44.39 1.97 40.44 48.27 1.00 3534 3110
Further Distributional Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma 6.86 0.51 5.95 7.95 1.00 3840 2689
Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).We can easily compare the fit of the three models using leave-one-out cross-validation.
loo(fit1, fit2, fit3)Output of model 'fit1':
Computed from 4000 by 100 log-likelihood matrix.
Estimate SE
elpd_loo -336.2 7.0
p_loo 4.6 0.8
looic 672.5 13.9
------
MCSE of elpd_loo is 0.0.
MCSE and ESS estimates assume MCMC draws (r_eff in [0.6, 1.1]).
All Pareto k estimates are good (k < 0.7).
See help('pareto-k-diagnostic') for details.
Output of model 'fit2':
Computed from 4000 by 100 log-likelihood matrix.
Estimate SE
elpd_loo -370.1 5.6
p_loo 2.5 0.3
looic 740.2 11.2
------
MCSE of elpd_loo is 0.0.
MCSE and ESS estimates assume MCMC draws (r_eff in [0.8, 1.0]).
All Pareto k estimates are good (k < 0.7).
See help('pareto-k-diagnostic') for details.
Output of model 'fit3':
Computed from 4000 by 100 log-likelihood matrix.
Estimate SE
elpd_loo -336.5 7.1
p_loo 4.8 0.8
looic 672.9 14.1
------
MCSE of elpd_loo is 0.0.
MCSE and ESS estimates assume MCMC draws (r_eff in [0.7, 1.3]).
All Pareto k estimates are good (k < 0.7).
See help('pareto-k-diagnostic') for details.
Model comparisons:
elpd_diff se_diff
fit1 0.0 0.0
fit3 -0.2 0.2
fit2 -33.8 6.7 The monotonic model fits better than the continuous model, which is
not surprising given that the relationship between income
and ls is non-linear. The monotonic and the unordered
factor model have almost identical fit in this example, but this may not
be the case for other data sets.
Setting Prior Distributions
In the previous monotonic model, we have implicitly assumed that all differences between adjacent categories were a-priori the same, or formulated correctly, had the same prior distribution. In the following, we want to show how to change this assumption. The canonical prior distribution of a simplex parameter is the Dirichlet distribution, a multivariate generalization of the beta distribution. It is non-zero for all valid simplexes (i.e., \(\zeta_i \in [0,1]\) and \(\sum_{i = 1}^D \zeta_i = 1\)) and zero otherwise. The Dirichlet prior has a single parameter \(\alpha\) of the same length as \(\zeta\). The higher \(\alpha_i\) the higher the a-priori probability of higher values of \(\zeta_i\). Suppose that, before looking at the data, we expected that the same amount of additional money matters more for people who generally have less money. This translates into a higher a-priori values of \(\zeta_1\) (difference between ‘below_20’ and ‘20_to_40’) and hence into higher values of \(\alpha_1\). We choose \(\alpha_1 = 2\) and \(\alpha_2 = \alpha_3 = 1\), the latter being the default value of \(\alpha\). To fit the model we write:
prior4 <- prior(dirichlet(c(2, 1, 1)), class = "simo", coef = "moincome1")
fit4 <- brm(ls ~ mo(income), data = dat,
prior = prior4, sample_prior = TRUE)The 1 at the end of "moincome1" may appear
strange when first working with monotonic effects. However, it is
necessary as one monotonic term may be associated with multiple simplex
parameters, if interactions of multiple monotonic variables are included
in the model.
summary(fit4) Family: gaussian
Links: mu = identity; sigma = identity
Formula: ls ~ mo(income)
Data: dat (Number of observations: 100)
Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup draws = 4000
Regression Coefficients:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept 30.82 1.41 28.00 33.56 1.00 2900 2690
moincome 14.73 0.65 13.44 16.02 1.00 2680 2550
Monotonic Simplex Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
moincome1[1] 0.67 0.04 0.60 0.74 1.00 2559 1907
moincome1[2] 0.26 0.04 0.18 0.35 1.00 3147 2672
moincome1[3] 0.07 0.04 0.01 0.15 1.00 2473 1679
Further Distributional Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma 6.87 0.52 5.95 7.97 1.00 3016 2827
Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).We have used sample_prior = TRUE to also obtain draws
from the prior distribution of simo_moincome1 so that we
can visualized it.
plot(fit4, variable = "prior_simo", regex = TRUE, N = 3)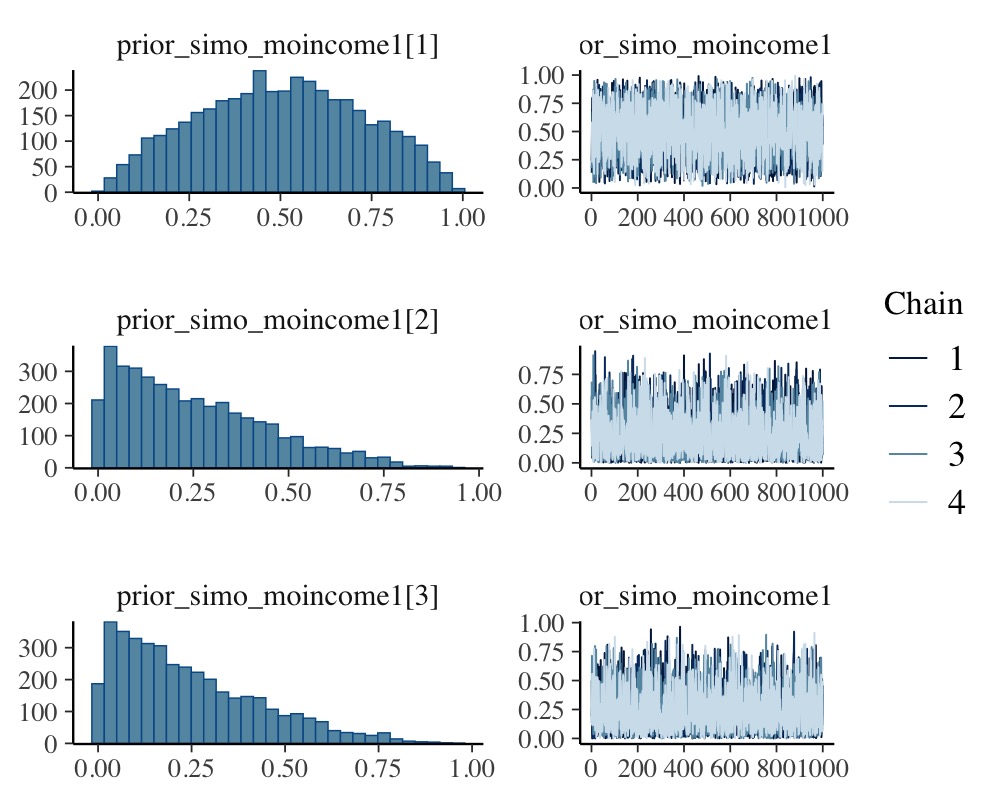
As is visible in the plots, simo_moincome1[1] was
a-priori on average twice as high as simo_moincome1[2] and
simo_moincome1[3] as a result of setting \(\alpha_1\) to 2.
Modeling interactions of monotonic variables
Suppose, we have additionally asked participants for their age.
dat$age <- rnorm(100, mean = 40, sd = 10)We are not only interested in the main effect of age but also in the
interaction of income and age. Interactions with monotonic variables can
be specified in the usual way using the * operator:
summary(fit5) Family: gaussian
Links: mu = identity; sigma = identity
Formula: ls ~ mo(income) * age
Data: dat (Number of observations: 100)
Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup draws = 4000
Regression Coefficients:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept 38.23 6.22 27.32 51.46 1.00 1271 2044
age -0.18 0.15 -0.50 0.08 1.00 1249 1768
moincome 11.31 2.75 5.66 16.32 1.00 1120 2224
moincome:age 0.09 0.07 -0.04 0.23 1.00 1145 2134
Monotonic Simplex Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
moincome1[1] 0.69 0.11 0.46 0.90 1.00 1593 1525
moincome1[2] 0.24 0.10 0.03 0.44 1.00 1677 1729
moincome1[3] 0.07 0.05 0.00 0.19 1.00 2570 1713
moincome:age1[1] 0.47 0.25 0.03 0.90 1.00 1702 2001
moincome:age1[2] 0.33 0.22 0.01 0.82 1.00 2035 2170
moincome:age1[3] 0.20 0.17 0.01 0.67 1.00 1921 2258
Further Distributional Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma 6.84 0.51 5.92 7.92 1.00 3078 2408
Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).
conditional_effects(fit5, "income:age")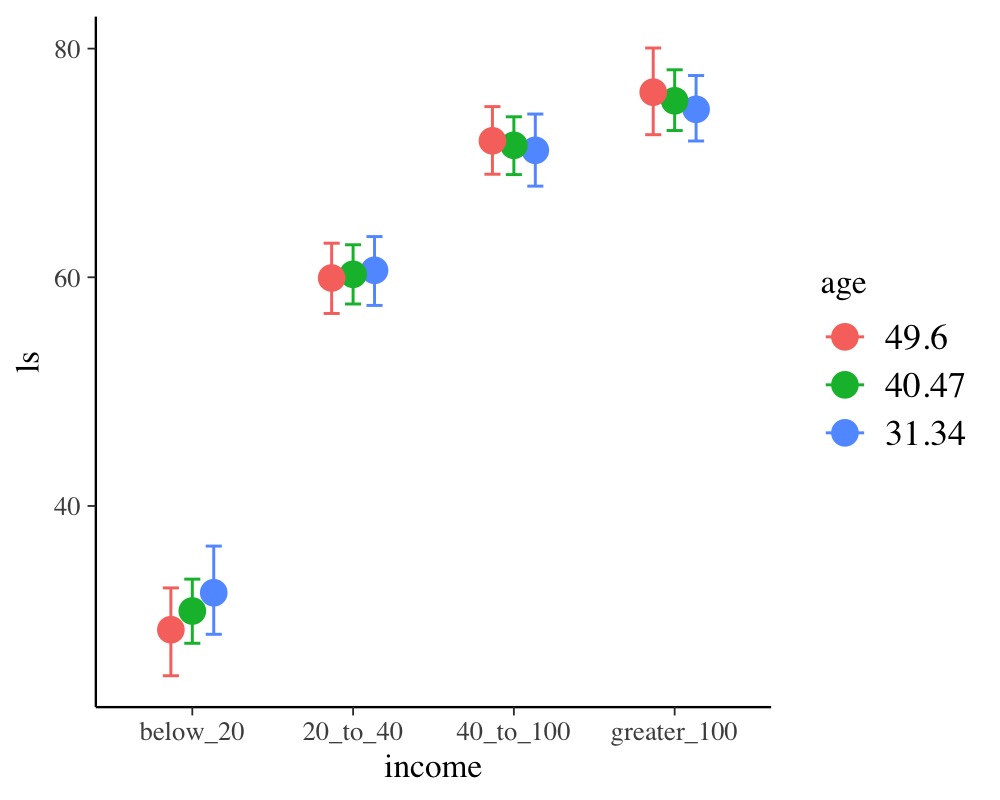
Modelling Monotonic Group-Level Effects
Suppose that the 100 people in our sample data were drawn from 10
different cities; 10 people per city. Thus, we add an identifier for
city to the data and add some city-related variation to
ls.
dat$city <- rep(1:10, each = 10)
var_city <- rnorm(10, sd = 10)
dat$ls <- dat$ls + var_city[dat$city]With the following code, we fit a multilevel model assuming the
intercept and the effect of income to vary by city:
summary(fit6) Family: gaussian
Links: mu = identity; sigma = identity
Formula: ls ~ mo(income) * age + (mo(income) | city)
Data: dat (Number of observations: 100)
Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup draws = 4000
Multilevel Hyperparameters:
~city (Number of levels: 10)
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sd(Intercept) 12.95 3.78 7.52 21.13 1.00 1210 2249
sd(moincome) 1.56 1.11 0.08 4.22 1.00 938 1982
cor(Intercept,moincome) -0.26 0.46 -0.93 0.80 1.00 2598 1934
Regression Coefficients:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept 43.42 9.03 26.47 61.52 1.00 1208 1850
age -0.29 0.19 -0.65 0.06 1.00 1214 2517
moincome 9.22 3.43 2.83 15.70 1.00 1194 2199
moincome:age 0.13 0.08 -0.02 0.29 1.00 1186 2272
Monotonic Simplex Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
moincome1[1] 0.58 0.16 0.18 0.84 1.00 1441 1566
moincome1[2] 0.32 0.15 0.06 0.67 1.00 1691 1881
moincome1[3] 0.10 0.08 0.01 0.32 1.00 2076 1937
moincome:age1[1] 0.59 0.23 0.06 0.93 1.00 1596 2033
moincome:age1[2] 0.27 0.19 0.01 0.74 1.00 2203 2364
moincome:age1[3] 0.15 0.15 0.00 0.60 1.00 2305 2108
Further Distributional Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma 6.39 0.52 5.45 7.49 1.00 3000 3133
Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).reveals that the effect of income varies only little
across cities. For the present data, this is not overly surprising given
that, in the data simulations, we assumed income to have
the same effect across cities.
References
Bürkner P. C. & Charpentier, E. (in review). Monotonic Effects: A Principled Approach for Including Ordinal Predictors in Regression Models. PsyArXiv preprint.